数据类型与存储
参考链接:https://www.midlane.top/wiki/pages/viewpage.action?pageId=26183116
1.补码与浮点数
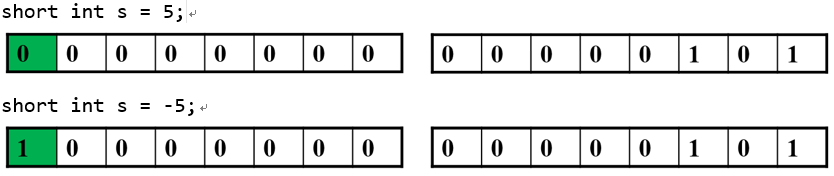
计算机采用二进制表示数据,但是从数学意义上,使用二进制并不能表示负数。因为二进制每一位的权值都大于0。为了解决这个问题,人们在二进制数据上使用了符号位,通过符号位来表示数据的正负。符号位是数据的最高位,当这一位为0时,表示数据是正数,而符号位为1时,则表示这个数是负数。
以short类型为例,通过下面两个示意图,可以看出符号位的作用:
1.1 原码、反码、补码
原码:第一位表示符号位,其余位表示绝对值大小。
1 2
[+1]原 = 0000 0001 [-1]原 = 1000 0001
反码:正数的原码是其本身,负数的反码是符号位不变,其余位取反。
1 2
[+1] = [00000001]原 = [00000001]反 [-1] = [10000001]原 = [11111110]反
补码:正数的原码是其本身,负数的补码是除符号位外其余各位取反后加1。
1 2
[+1] = [00000001]原 = [00000001]反 = [00000001]补 [-1] = [10000001]原 = [11111110]反 = [11111111]补
为什么会有反码和补码呢?原因是方便负数运算,计算机并没有减法器,使用补码可以让加减法都能用上加法器,简便了计算机基本电路,同时也解决了0在计算机中表示问题。
举例说明
1
2
[+1]原 = 0000 0001
[-1]原 = 1000 0001
计算1+(-1)的结果应该为0,可此时二进制运算完后为1000 0010,转换十进制为-2,这显然是不对的,再来看看反码的运算:
1
2
+1的反码为 0000 0001
-1的反码为 1111 1110
计算的结果为反码 [1111 1111],转换为原码为[1000 0000],最后结果为-0,0带符号是没有意义的。再看看补码的运算
1
2
+1的补码,同原码 为0000 0001
-1的补码,反码 +1 为1111 1111
得到结果为 1 0000 0000,此时已经超过了8位舍去为0000 0000,它的原码也是0,问题解决
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
1
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示。
注:补码转换为原码的方式为:
补码的补码,就是原码(^_^)…
1.2 使用补码的意义
对于有符号数,由于最高位表示数据的符号位,那么在参与计算时,这一位是不能参与数值运算的,这对CPU来说,无疑是增加了设计的复杂度,因为计算机的各种计算都需要通过硬件电路来实现的,多一种特殊情况要考虑,设计的复杂度就增加一分。而采用补码的方式,则可以让计算机“忽略”符号位,在计算时,让符号位也可以直接参与数值运算。
1.3 有符号数的存储
对于正数来说,直接存储其原码即可,这样存储没有问题,但对于负数,这样的存储方式并不是最佳方式。对于负数,计算机存储的实际是数据的补码。
实际上对于正数,原码与补码一致,因此可以理解为有符号数存储的都是其补码
1.4 浮点数的存储
浮点数在内存中需要以指数的形式存储,比如: float f = 3.1415926 = 0.31415926 * 10^1
那么,该数在内存中可以按下面的方式存储:
| 1bit符号位 | 底数部分 | 指数部分 |
|---|---|---|
| + | .31415926 | 1 |
对于float类型来说,4个字节共32位中,究竟多少位用于表示底数部分,多少位用于表示指数部分,C标准并无具体的规定,由各编译器的实现来决定的。底数部分越多,则精度越高,指数部分越多,则能表示的范围越大。
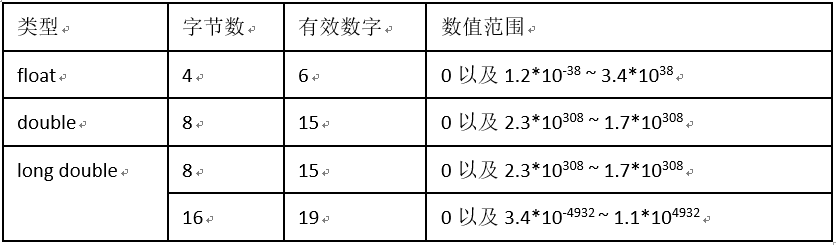
1.5 数据表示范围
计算机的内存终归有限,所以计算机不能存储一个无限大的整数,也不能存储一个无限精度的小数(比如0.11这样无法转化成2进制的数),用有限的内存去存储数据,我们需要知道数据的存储范围。
这里只讨论浮点数的数据表示范围:
对于浮点数,由于其存储的是指数与底数,所以还我们还需要衡量它的存储精度,一般用有效数字来表示,也由于浮点数存储不准确性(浮点数存储0.11时会有精度丢失),所以浮点数只可以进行范围大小的比较,不可以判断相等。
1.6 浮点数的比较
尤其注意,浮点数不可以使用 == 运算符去判断两个浮点数相等,并不是C语言语法规定不可以,而是实际运算的结果不准确,如下:
1
2
3
4
float num = 0.11;
if(num == 0.11) { //这里实际上 num并不等于 0.11,因为num在存储到内存之后丢失精度
… //这段语句不会执行到
}
基于以上特点,对浮点数进行比较时,只可以对两浮点数在一定精度内进行比较,以两数之差的绝对值小于某个精度时作为判断依据,如下:
1
2
3
4
5
6
7
8
#include <math.h> //fabs()头文件
#define LIMIT 1e-6 // 精度
float num = 0.11;
if(fabs(num – 0.11) < LIMIT) { //通过比较两浮点数之差的绝对值与规定精度判断浮点数相等
…
}
2.位运算
见位运算篇
3.常量
3.1 常量表示
程序运行过程中值不会改变的量称为常量,比如立即数,字符,数组名,字符串等。
3.2 常量存储
注意,与变量不一样,并不是所有的常量都会占用栈空间,比如数组名就没有专门的存储地地方。而字符串常量则只存储在程序的只读数据段。有的常量还可以在编译时直接编译机器的指令里。
1
2
int a = 2; // 2可以作为指令中的立即数存储在代码区
printf("%d", 100); // 100可能存储在程序的数据区
3.3 常量类型
常量也具有类型,默认情况下按如下进行处理:
- 程序中所有出现的浮点数都是double类型。
- 单个字符与整数默认是int类型。
- 如果整数超出了int的表示范围,它将被当作long 或 long long来处理。
如果想改变常量的类型,则可以在常量后面添加指定后缀u l f L,如下:
1
2
3
4
5
6
7
8
9
123 // int类型
123L或123l // long类型
123LL // long long类型
123u // unsigned int 类型
123ul // unsigned long
123ull // unsigned long long
3.14 // double类型
3.14f // float类型
3.14L // long double类型
4.静态变量
静态变量存储在数据段,但是静态变量要在第一次调用时才会创建,然后在程序的整个运行期间都存在。示例如下:
1
2
3
4
5
6
7
8
9
10
11
void fun()
{
static int i = 0; //第一次调用fun()时创建并赋值,后面再次调用时不再创建,直接使用上次保存的值
i++;
}
int main()
{
fun(); // i = 0
fun(); // i = 1
}